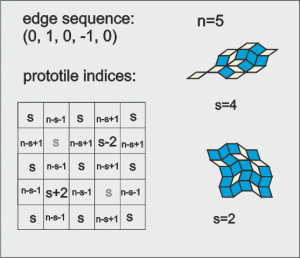
A rhomb tiling based on our tiling model is determined by the choise of the edge sequence ![]() , i.e. the sequence of prototile edge angles along the substitution tile edge in units of
, i.e. the sequence of prototile edge angles along the substitution tile edge in units of ![]() . The configuration of the basic substitution tile can be represented by the substitution tile matrix
. The configuration of the basic substitution tile can be represented by the substitution tile matrix
(1) 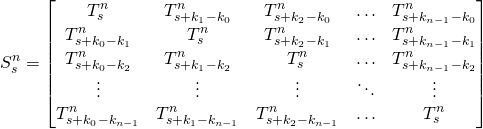
![]() denotes a prototile with opening angle
denotes a prototile with opening angle ![]() in units of
in units of ![]() and
and ![]() the corresponding substitution tile. The matrix representation is possible because always four tiles meet at a vertex. The rhomb tiles along a row or a column are connected to each other by opposite and parallel edges. These chains of tiles are called worms.
the corresponding substitution tile. The matrix representation is possible because always four tiles meet at a vertex. The rhomb tiles along a row or a column are connected to each other by opposite and parallel edges. These chains of tiles are called worms.
Worms are very usefull in the construction of the substitution tiles as is illustrated below for a specific example. At the upper left corner one starts with a prototile having the same opening angle ![]() as the substitution tile. To the right prototiles are added with opening angles
as the substitution tile. To the right prototiles are added with opening angles ![]() , such that the upper and lower edge of the worm follow the edge sequence. For the next row the tiles have opening angle
, such that the upper and lower edge of the worm follow the edge sequence. For the next row the tiles have opening angle ![]() , etc. This procedure becomes more complex if the substitution rule involves the replacement of some of the prototiles with opening angle
, etc. This procedure becomes more complex if the substitution rule involves the replacement of some of the prototiles with opening angle ![]() by tiles with complementary opening angles
by tiles with complementary opening angles ![]() (marked somehow, for instance by means of a different colour). Nevertheless it is just a matter of thorough bookkeeping.
(marked somehow, for instance by means of a different colour). Nevertheless it is just a matter of thorough bookkeeping.
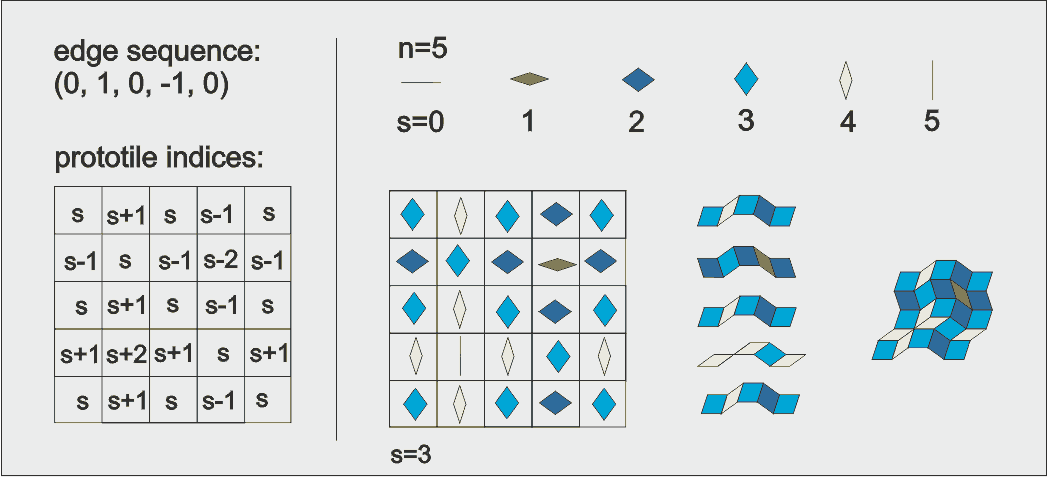
 edge sequence
edge sequence 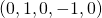 . the matrix filled in with prototiles for
. the matrix filled in with prototiles for 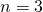 , the rows of prototiles connected into worms, and the worms connected into the substitution tile.
, the rows of prototiles connected into worms, and the worms connected into the substitution tile.This procedure becomes more complex if the substitution rule involves the replacement of some of the prototiles with opening angle ![]() by tiles with complementary opening angles
by tiles with complementary opening angles ![]() . A motivation to do this is to reduce the of tiles in the basis set to the even
. A motivation to do this is to reduce the of tiles in the basis set to the even ![]() tiles in the odd
tiles in the odd ![]() case. In the above example for instance this may be accompliced by replacing all odd tiles in odd rows and columns by
case. In the above example for instance this may be accompliced by replacing all odd tiles in odd rows and columns by ![]() tiles and the even tiles in odd rows and colums, occurring at their crossing points, by tiles rotated over
tiles and the even tiles in odd rows and colums, occurring at their crossing points, by tiles rotated over ![]() . The basis set is reduced to two tiles instead of four, as shown in the next figure.
. The basis set is reduced to two tiles instead of four, as shown in the next figure.
The above procedure uses the rhomb prototiles as building blocks. An alternative way to construct the tiles is to draw a supertile grid, as is illustrated below. First, a sufficiently large supertile edge curve is constructed by applying the substitution rule repeatedly to the original edge sequence. This edge curve is used to draw the circumference of the supertiles. Next, duplicates of the edge curve are placed between all opposite break points of the circumference in both directions. The resulting grid encloses the prototiles making up the substitution tile. This construction procedure is not very suitable for the next generation of supertiles. To produce a large patch of a tiling one mighty proceed as follows. First the substitution tile edge is used to construct the edge of the next several generations of supertiles.This supertile edge then is used to draw the prototilegrid in the same way as was done for the first generation substitution tile. This construction procedure is no doubt the faster one. However, if the prototiles are to be decorated, for instance by a particular color, it is less suitable than the previous one.
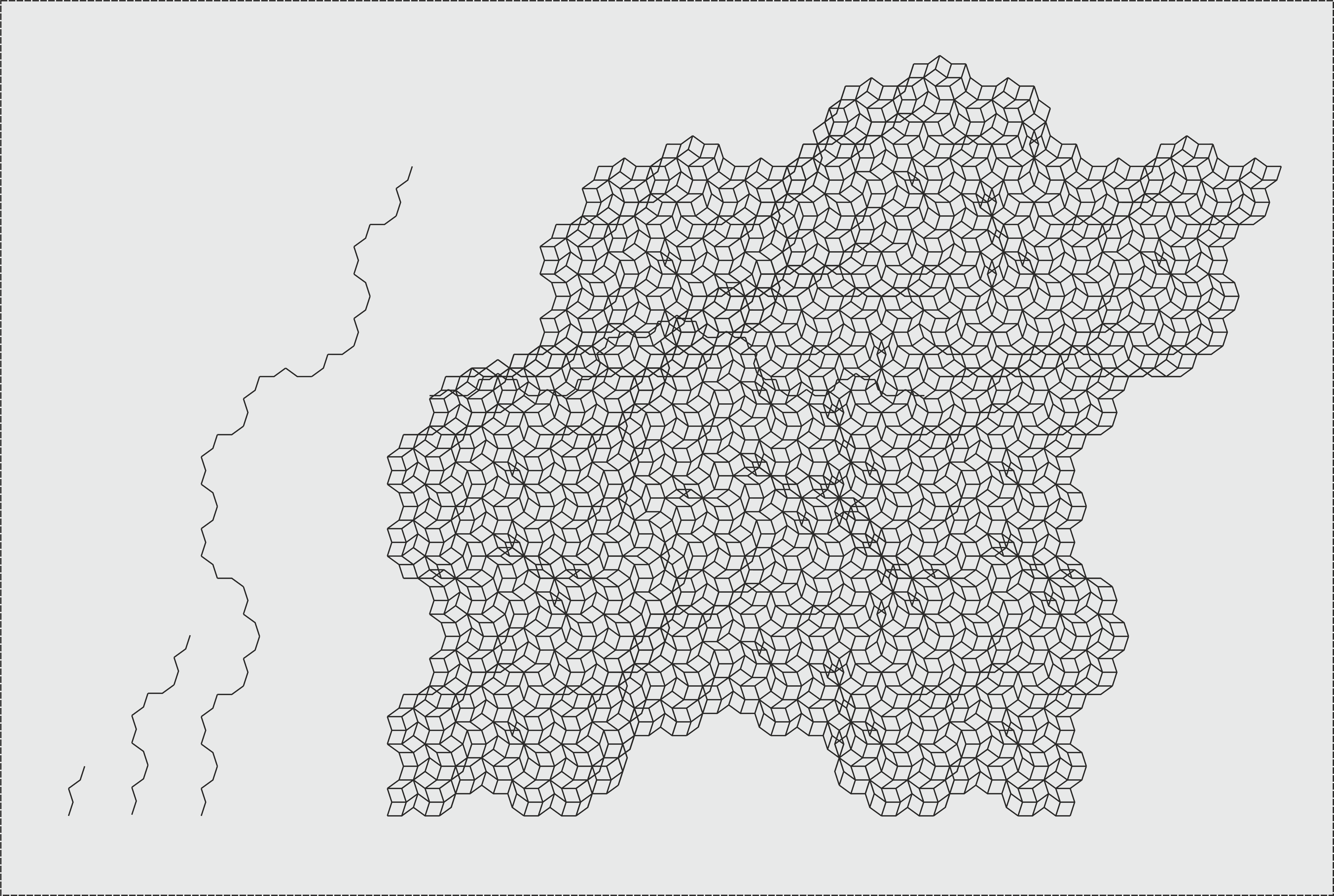
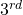 generation
generation 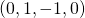 or Koch supertile for
or Koch supertile for 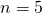 and
and 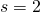 .
.