Space can be filled with a combination of tetrahedra and octahedra. This tetrahedral-octahedral honeycomb consists of alternating isohedral tetrahedrons and octahedrons in a ratio of 2:1.
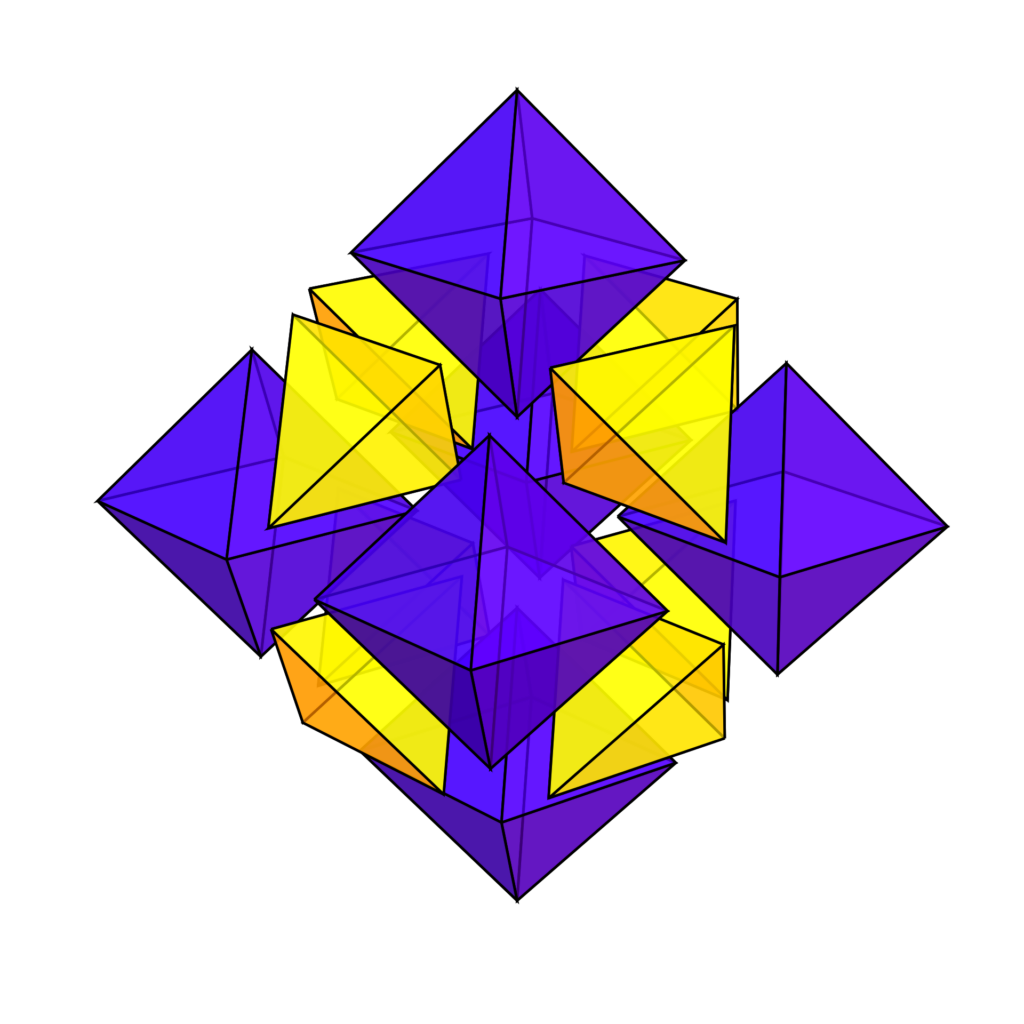
In crystal structure terminology the vertices form an fcc structure. The vertices are at the corners and the face centers of the cubic unit cell. At each vertex corners of 8 tetrahedra and 6 octahedra meet. Edges ar common two 2 tetrahedra and 2 octahedra.
Disorder on an fcc lattice
Elements having the fcc structure are aluminium, copper, silver and gold. Some alloys of these metals are disordered and have an average fcc structure , for instance Cu![]() Au. The two types of metal atoms are more or less randomly ditributed over equivalent sites. However, locally the occupation of the sites may be ordered to some extent if x has a particular value, for instance one, two or one half, because in that case tetrahedral or octahedral clusters of nearest neighbor atoms may have the bulk composition, allowing for short range order.
Au. The two types of metal atoms are more or less randomly ditributed over equivalent sites. However, locally the occupation of the sites may be ordered to some extent if x has a particular value, for instance one, two or one half, because in that case tetrahedral or octahedral clusters of nearest neighbor atoms may have the bulk composition, allowing for short range order.
The author of this website is interested in this problem, because in the seventies of the previous century he spent quite some time on the study of the disordered structure of solid electrolyte materials by diffuse X-ray diffraction. One of these materials was HgAg2I4. In its ionically conducting high temperature phase the cations occupy the sites of an fcc structure in a disordered fashion. At the time we published some qualitative diffuse scattering pictures for this phase (T. Hibma et al. Journal of Physics C Solid State Physics 9(9):1691). An artists view of the pattern in reciprocal space is shown in the picture below.
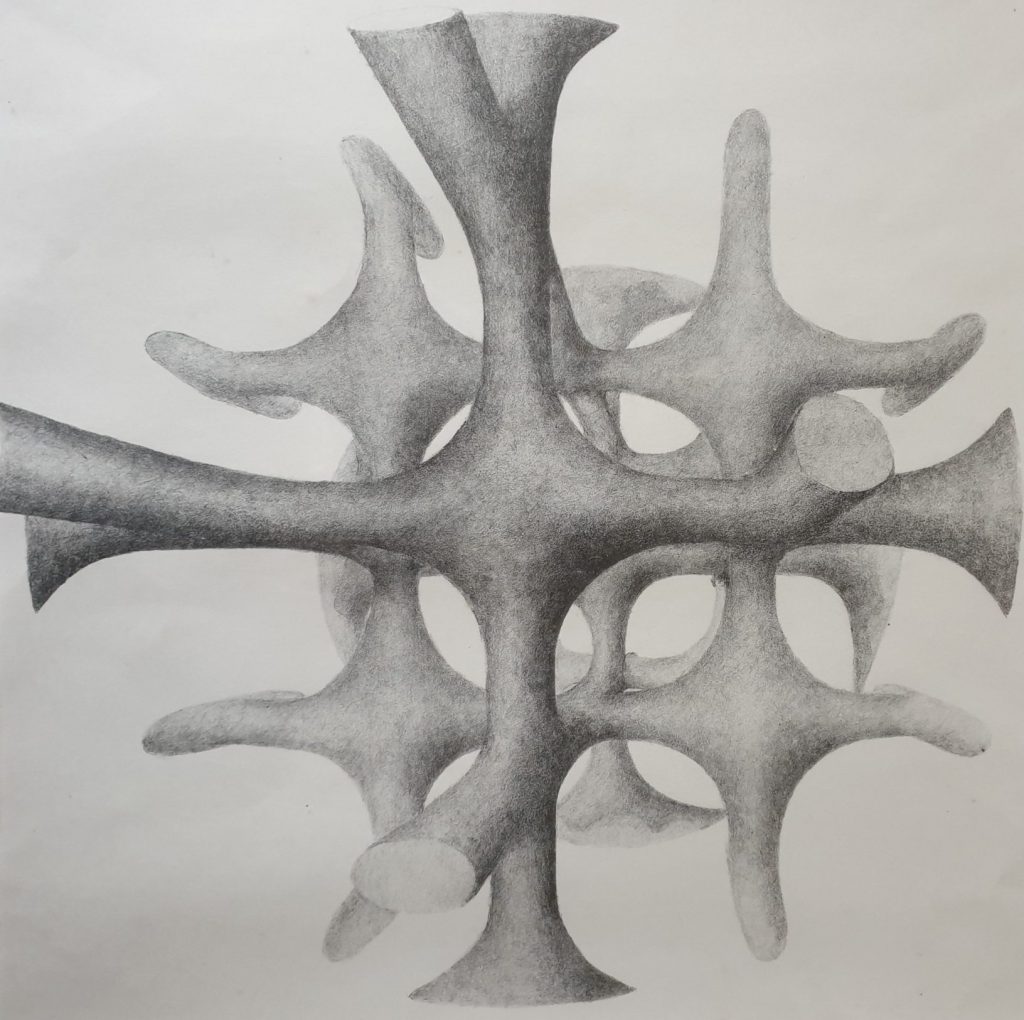
Many years later we discovered that a rather simple explanation of this pattern could be formulated using the cluster model of de Ridder et al. Acta Cryst. A32, 216 (1976). They showed that if a structure is disordered, and the local distribution in small clusters has precisely the bulk composition, the locus of the diffuse scattering is in general given by
(1) ![]()
where ![]() is the number of vertices of the cluster,
is the number of vertices of the cluster, ![]() is the reciprocal lattice vector and
is the reciprocal lattice vector and ![]() the position vector of the vertices.
the position vector of the vertices.
In the case of tetrahedral clusters the locus of the diffuse intensity is
(2) ![]()
The lines given by this formula are, in fact, the lines of maximum intensity in the picture. This implies that in HgAg2I4 each tetrahedron site is very nearly occupied by two Ag-ion, one Hg-ion and one vacancy. On the fcc lattice neighboring tetrahedra have two sites in common. The disorder is, therefore, restricted to the orientation of pairs of ions/vacancy on opposite edges.
We now return to the general problem. Special cases of interest are the compositions ![]() or
or ![]() , because one then may require that the composition of the tetrahedra is equal to the bulk composition. Similarly, the compositions
, because one then may require that the composition of the tetrahedra is equal to the bulk composition. Similarly, the compositions ![]() ,
, ![]() or
or ![]() may be satisfied by a corresponding occupation of the octahedra. In the following we will explore the consequences for the type of long range order if the cluster (t or o) composition is equal to the average bulk composition.
may be satisfied by a corresponding occupation of the octahedra. In the following we will explore the consequences for the type of long range order if the cluster (t or o) composition is equal to the average bulk composition.
![]()
Because both polyhedra have an even number of vertices, both the tetrahedra and the octahedra may satisfy the bulk composition requirement. For the tetrahedron only a single configuration is possible, but for the octahedron there are two possibillities, all three atoms of the same kind occupy neighboring sites, or two atoms occupy neighboring sites and the third a site opposite to one of them.
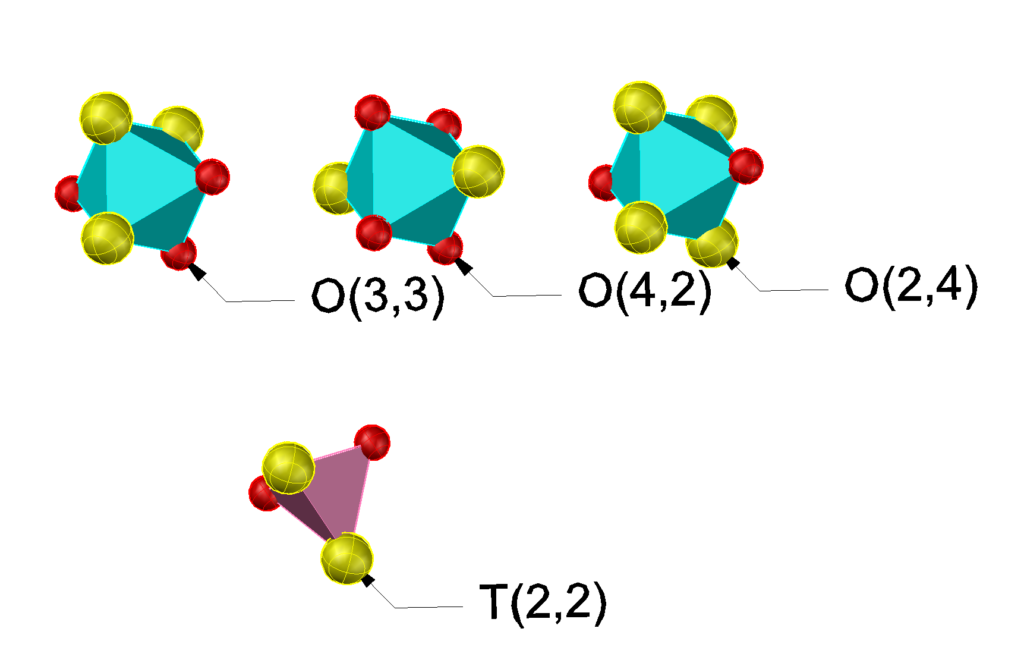
Because the T and O have a face in common only the prototile denoted by prototiles shown in the figure are allowed. Selecting only the T(2,2) and O(3,3) tiles forces the ordered stucture shown below.
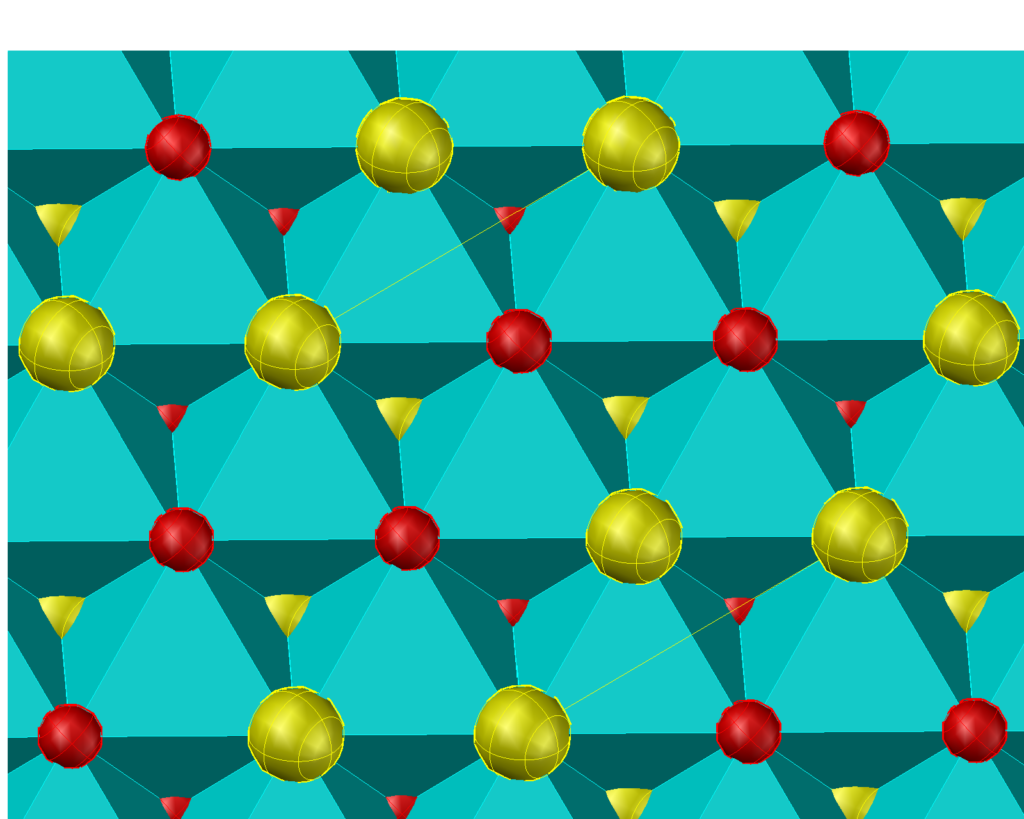
Similarly, if we select only the T(2,2) and the O(4,2) and O(2,4) another forced ordered structure, the socalled CuAu structure is obtained.
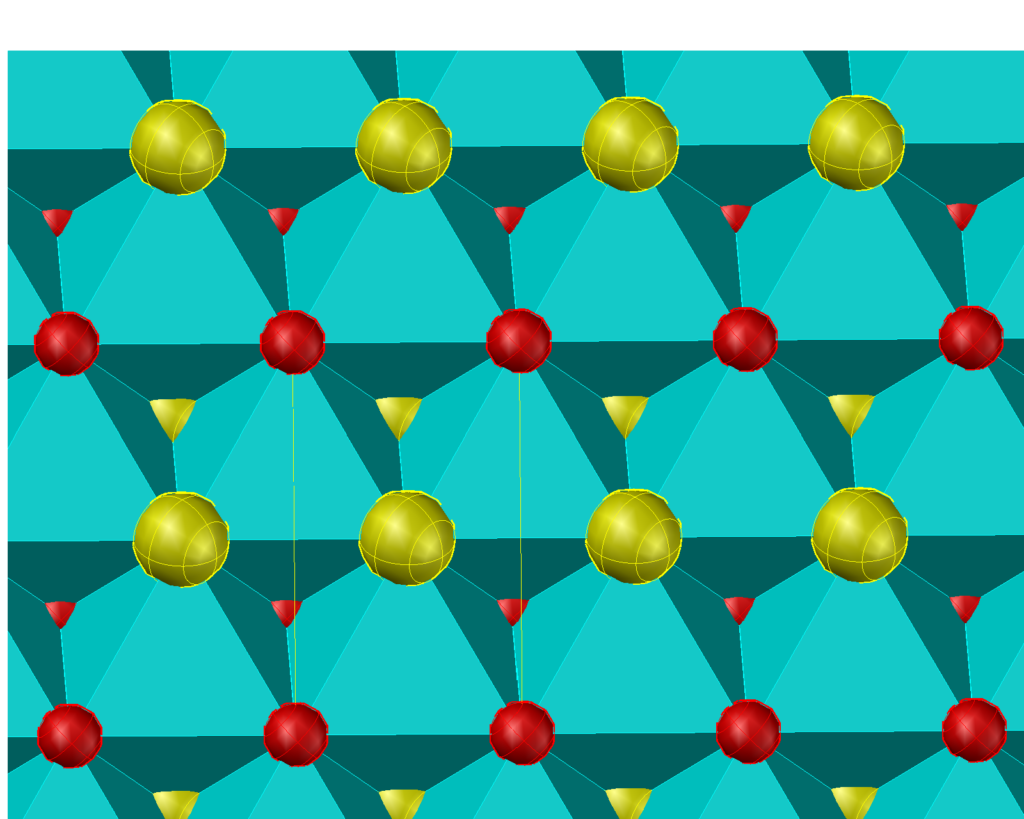
If both the O(2,4)/O(4,2) and the O(3,3) prototiles are admitted a disordered structure is obtained.
The question we now want to answer is, whether it is possible to find a subset of these O and T tiles and a substitution rule to build a non-periodic 3d tiling.
A big tetrahedron (BT) and a big octahedron (BO) twice as large in all directions may be constructed using four T and one O prototile for the BT and 8 T and 6 O prototiles for the BO.
If the composition of T is equal to the bulk composition, four different BT are possible, two BT using an O(3,3) and two using either an O(4,2) or an O(2,4). The BO have either a central A or B atom. In either case there are two possibble formations of the eight T around the central atoms. In the most symmetric case two O(4,2) or O(2,4) must be added at opposite positions, in the less symmetric case four O(3,3). The remaining four, resp. two O prototiles may be chosen to be either an O(3,3) or an O(4,2)/O(2,4) tile. The possible big tiles in terms of T prototiles are shown in the drawing below.
(still under construction)