Most tilings of the plane are periodic. Common examples are pavements of roads or sidewalks, the surface of a brick wall, the tile pattern of kitchen or bathroom floors. In aperiodic tilings the pattern does not repeat itself. Since a few decades an increasing number of aperiodic tilings, constructed using only a few different tiles and a prescription how the tiles should be put together, have been found. The most famous among them is the Penrose tiling with a five-fold rotation symmetry, discovered in the early seventies. One version, shown in Fig I1 is the tiling built using two different rhombs with opening angles 
and 
. The red dots are decorations of these so-called prototiles to indicate how they should be connected.
Another example of aperiodic tiling is the Amman Beenker (AB) tiling, also based on two rhomb tiles with opening angle 
and 
. A simple way to construct aperiodic tilings is to use a substitution rule. The substitution rule tells us how inflated copies of a basic set of tiles are decomposed into a discrete number of basic tiles. By iteratively applying the rule to the inflated tiles an arbirary large tiling is obtained. The basic tiles, in our case the two rhomb tiles, are called the prototiles, and the (multiply) inflated tiles the supertiles.
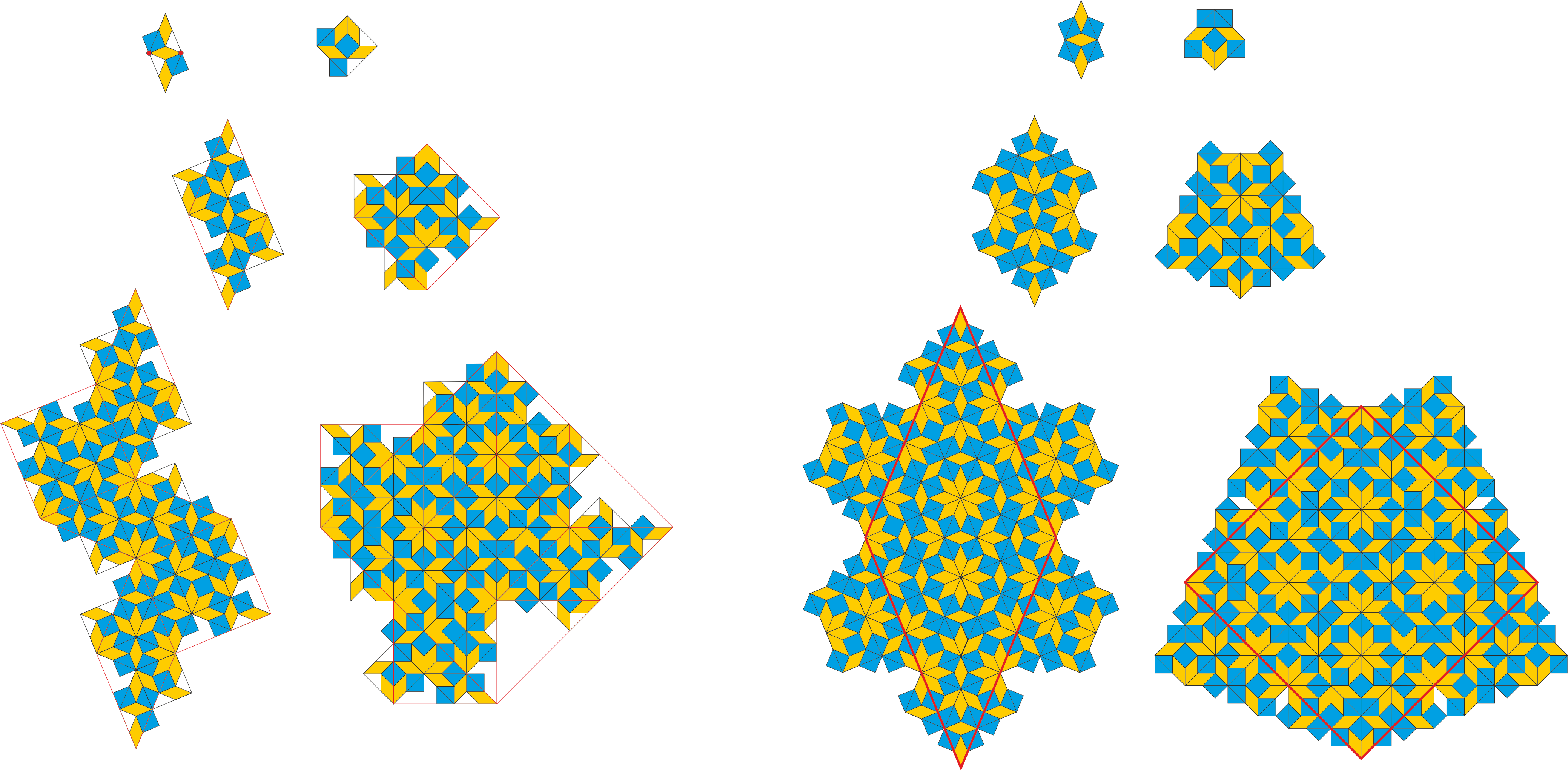
In Fig. I2 three generations of substitution tiles are shown for the AB tiling, to the right the commonly used partly overlapping tiles, and on the left hand side the corresponding area conserving tiles The substitution edge angles are 
respectively. The number set 
is the so called edge sequence.
The above and many other substitution tilings are depicted in the aperiodic tilings encyclopedia by E.O.Harriss and D. Frettlöh. Other useful links are the wikipedia page on aperiodic tilings and a list of aperiodic sets of tiles.