The cubic honeycomb is the only regular honeycomb in Euclidian 3-space. There are only 5 space-filling polyhedra using translations only, called parallelohedra. Three of them have cubic symmetry. They are the Wigner-Seitz cells of the primitive, body-centered and face-centered cubic lattices (see fig. 1)
The cube can be divided into 48 tetrahedra by the mirror planes of the cubic system. It is in fact a first type Hill tetrahedron
The basic tetrahedron of the primitive cube can be divided into two identical halves for the body-centered cubic Wigner-Seitz cell, or truncated octahedron, and into four identical basic polyhedra for the face-centered cubic Wigner-Seitz cell, the rhombic dodecahedron.
The truncated octahedron is not the only space filling polyhedron on a body centered cubic lattice, because the basic tetrahedron of the primitive cube can be divided into identical halves in many different ways by a separation plane containing the twofold axis connecting the two halves (fig.2). Two of the polyhedra obtained in this way are the Hill tetrahedra type 2 and 3.
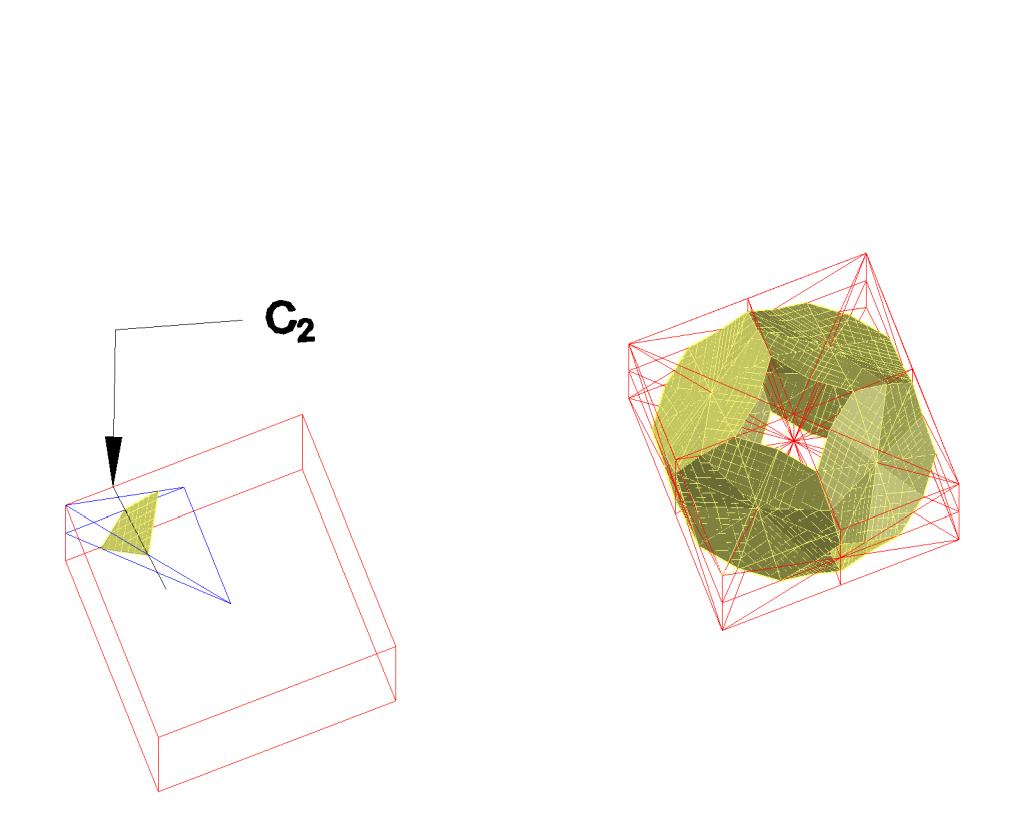
Right: By applying all possible cubic mirror planes an infinite polytopic surface is obtained, separating two congruent infinite polyhedra.
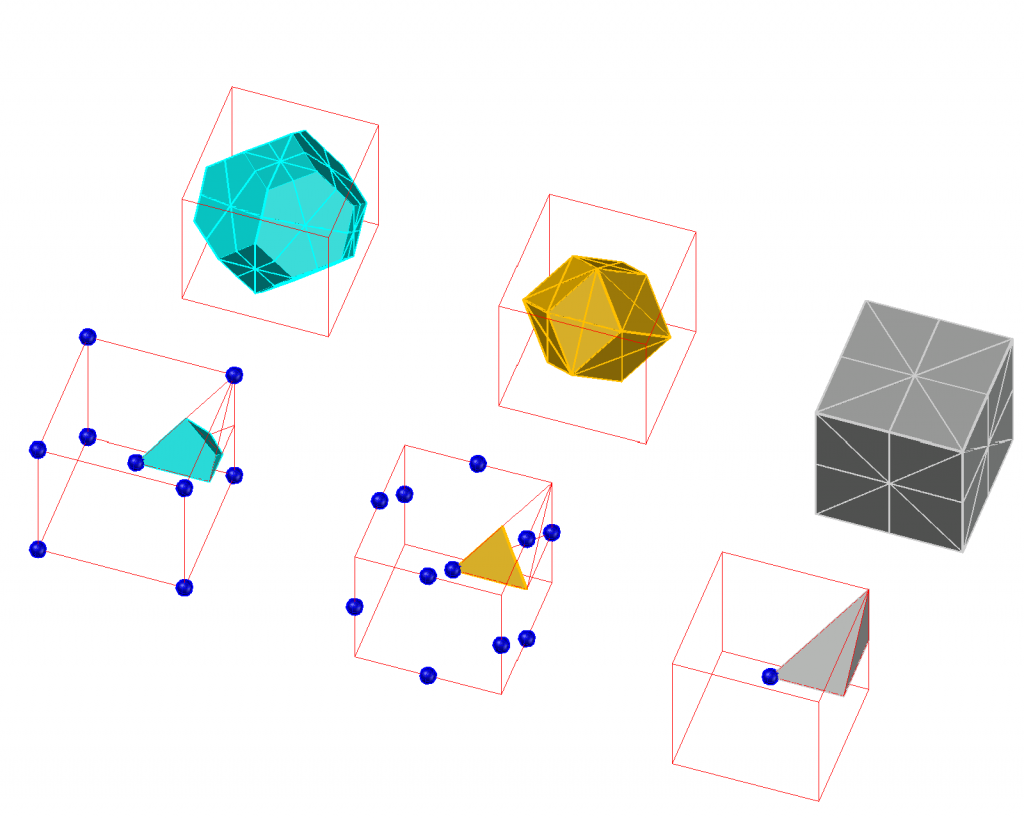
All examples of the bcc spacefilling polyhedra shown in fig.3 are non-convex in contrast to the truncated octahedron, the WS cell.
The magenta object is the well-known stellated rhombic dodecahedron, also known as the Escher solid. The basic tetrahedron is a combination of two basic tetrahedra of the fcc Wigner Seitz cell . The separation plane contains the face center of the cube. Its basic tetrahedron is a Hill type 2 tetrahedron.
The grey object is a cubic cross. The separation plane contains a point halfway the cube edge and a face center.
The orange object is special, because the separation plane contains the cube center. Its basic tetrahedron is a Hill type 3 tetrahedron. The honeycomb can alternatively be built by the space filling star-shaped hexadecahedron ( in projection looking like a wind rose) shown in the upper left part of the picture. In the space filling tiling six of these stars have a body diagonal of the cube in common. These stars fit into the slots at the cube edges. In fig. 4 resin prints of the wind-rose-like objects are shown.

The dividing surface does not have to be planar as long as it is also twofold rotation symmetric in the the way described previously. A famous example is the Schwartz primitive minimal surface . It looks somewhat like the yellow polyhedron, but the cross section with the cube surface is a circle instead of an octagon.
