Metallic means or ratios (https://en.wikipedia.org/wiki/Metallic_mean) are the largest roots of the polynomial
(1) ![]()
where ![]() is a nonnegative integer, i.e.
is a nonnegative integer, i.e.
(2) ![]()
The first four values are given in the table below. The ones for ![]() and
and ![]() are the well-known Golden and Silver means.
are the well-known Golden and Silver means.
| Metallic means | |||
|---|---|---|---|
| n | Ratio | Value | |
| 1: | (1 + √5)/2 | 1.618033989 | Golden |
| 2: | (2 + √8)/2= 1 + √2 | 2.414213562 | Silver |
| 3: | (3 + √13)/2 | 3.302775638 | (Bronze) |
| 4: | (4 + √20)/2= 2 + √5 | 4.236067978 |
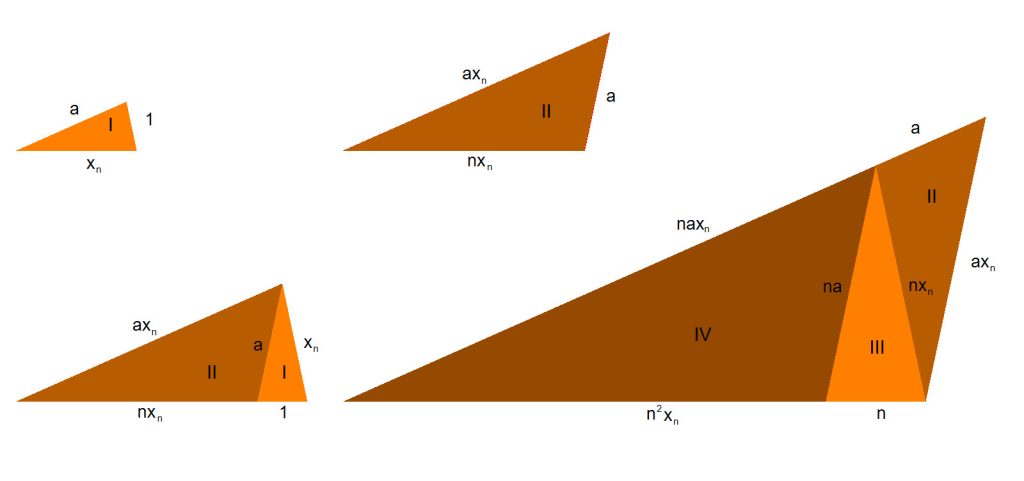
In the following we wil show that equation 1 may be used to construct pairs of triangles tiling the plane aperiodically by inflation, the inflation factor being the metallic mean ![]() . The basic triangle I has edges of length
. The basic triangle I has edges of length ![]() . Inflation by a factor
. Inflation by a factor ![]() gives a similar tile with edges of length
gives a similar tile with edges of length ![]() . Using eq. 1, the second edge may be split into line segments of length
. Using eq. 1, the second edge may be split into line segments of length ![]() and
and ![]() , which devide the triangle into two triangles, one congruent to the basic triangle I and another one, II, with edge lengths
, which devide the triangle into two triangles, one congruent to the basic triangle I and another one, II, with edge lengths ![]() . If tile II on its turn is inflated by a factor
. If tile II on its turn is inflated by a factor ![]() , a triangle with edge lengths
, a triangle with edge lengths ![]() ,
, ![]() and
and ![]() is obtained. This inflated type II triangle may be divided into
is obtained. This inflated type II triangle may be divided into ![]() prototiles I and
prototiles I and ![]() prototiles II, as shown in Fig. 1.
prototiles II, as shown in Fig. 1.
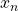 ,
, 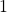 and
and  , and one with edge lengths
, and one with edge lengths 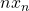 ,
,  and
and 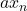 . The inflation factor is
. The inflation factor is 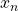 , the largest root of the polynomial
, the largest root of the polynomial 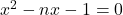 .
.  is a free parameter in the interval
is a free parameter in the interval 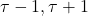 . Tiles III and IV are multiples of tiles I and II by a factor of
. Tiles III and IV are multiples of tiles I and II by a factor of 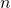 .
.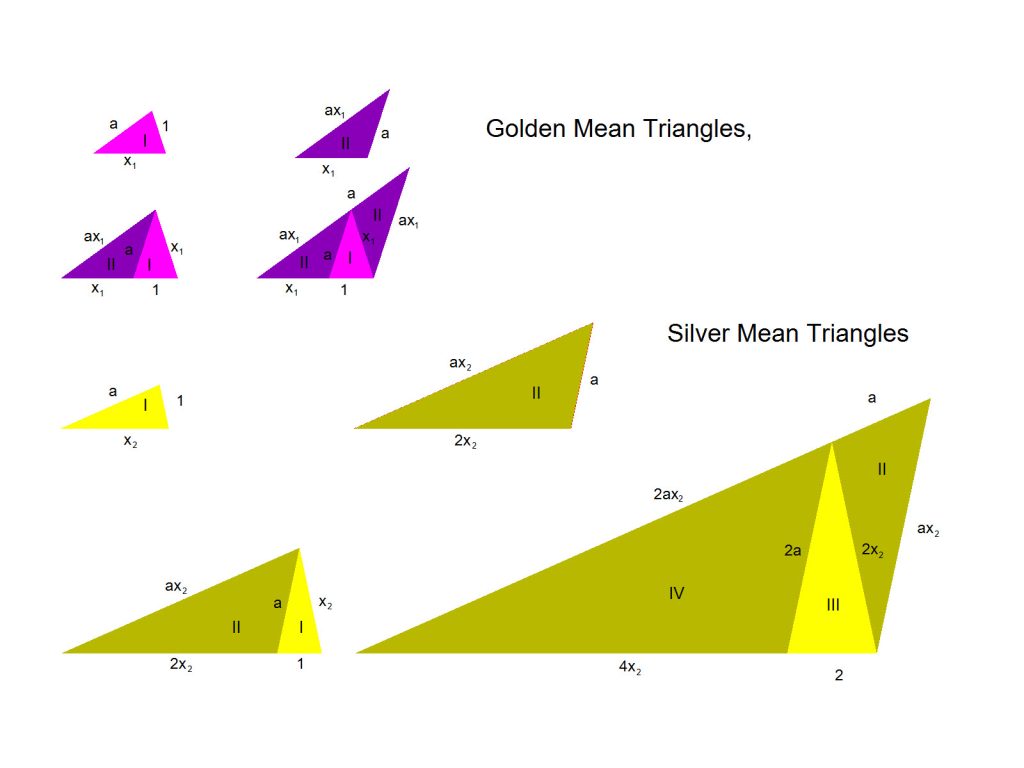
The tiles for ![]() are closely related to the famous Penrose tiles, because
are closely related to the famous Penrose tiles, because ![]() is the golden ratio. For
is the golden ratio. For ![]() the triangles I and II are the prototiles for the TübingenTriangle Tiling, while for
the triangles I and II are the prototiles for the TübingenTriangle Tiling, while for ![]() the Robinson triangles are obtained. (Note that the Penrose triangle substitution tiling does not fit into the above general substitution scheme although the prototiles are similar). Another special case is the Golden Triangle tiling. The value of a is
the Robinson triangles are obtained. (Note that the Penrose triangle substitution tiling does not fit into the above general substitution scheme although the prototiles are similar). Another special case is the Golden Triangle tiling. The value of a is ![]() in that case. (Fig. 2)
in that case. (Fig. 2)
Because ![]() is a free parameter, the “golden mean triangles” are a generalization of these Penrose type of tiles, with
is a free parameter, the “golden mean triangles” are a generalization of these Penrose type of tiles, with ![]() . Apart from the ones cited above, there is yet another special set of tiles, not mentioned in literature as such, i.e. the one for
. Apart from the ones cited above, there is yet another special set of tiles, not mentioned in literature as such, i.e. the one for ![]() , where
, where
(3) ![]()

These octahedra have three different types of faces, which are similar to the pair of golden mean prototiles with ![]() . In Fig.4 these “Danzer golden mean triangles” are shown as Zometool assemblies. The three octahedral faces are congruent to the two golden mean prototiles and one of the first inflated tiles, i.e. the smallest one at the lower left of fig.4
. In Fig.4 these “Danzer golden mean triangles” are shown as Zometool assemblies. The three octahedral faces are congruent to the two golden mean prototiles and one of the first inflated tiles, i.e. the smallest one at the lower left of fig.4

In Chapter 1 of Volume 2 of the book on Aperiodic Order edited by Baake and Grimm, Dirk Frettloeh discusses another very similar free parameter family of triangular inflation tilings originally introduced by Danzer. Its inflation factor is the largest root of the polynomial ![]() , i.e.
, i.e. ![]() =1.3247, the socalled plastic number. Because the polynomial is of the third degree, a third intermediate sized prototile is needed.
=1.3247, the socalled plastic number. Because the polynomial is of the third degree, a third intermediate sized prototile is needed.
Alternative for the Danzer ABCK Tiling.
The simplest tetrahedra having exclusively Danzer golden mean tiles as faces are the ones shown in fig.5. They may be connected to form a pyramid with a parallelogram as its base. The base is made up of three Danzer golden mean triangles. Because the height of the three tetrahedra is the same, their volume is proportional to the area of the bases of the individual tetrahedra, i.e. their volume ratios are ![]() .
.

These DEF tetrahedra are alternative prototiles for a tiling of space. To avoid confusion with the ABCK tiles of Danzer we will denote them by D, E and F. The third generation of substitution tiles may be constructed by a combination of second and first generation tiles as shown in fig. 6. The volumetric relationship is
(4) ![]()
(5) ![]()
(6) ![]()
Filling in the volume ratios of ![]() ,
, ![]() and
and ![]() , the volumes of
, the volumes of ![]() ,
, ![]() and
and ![]() are calculated to be proportional to
are calculated to be proportional to ![]() ,
,![]() and
and ![]() respectively, as they should.
respectively, as they should.

We have chosen the sets of prototiles in such a way that the substitution tiles have the same point group symmetry as their corresponding prototiles, i.e. ![]() for tiles F and D and
for tiles F and D and ![]() for tile E. The faces of the substitution tiles are all similar planar aperiodic Danzer golden mean tilings. Note that the faces of the Danzer octahedra are very different because they also contain dissimilar faces of the ABCK tetrahedra.
for tile E. The faces of the substitution tiles are all similar planar aperiodic Danzer golden mean tilings. Note that the faces of the Danzer octahedra are very different because they also contain dissimilar faces of the ABCK tetrahedra.