The formulae derived in the rhomb tile model can also be applied to isosceles triangles with opening angles ![]() ,
, ![]() , because the triangles are congruent to half rhombs. The dents and dimples may be removed from the substitution tile edges, making them straight and no crossing of edges can occur. It is, therefore, easier to avoid negative tiles, If one in addition gives up the face-to-face tiling principle, the chances to tile the plane with positive tiles becomes even larger. Known examples are the Robinson triangles (
, because the triangles are congruent to half rhombs. The dents and dimples may be removed from the substitution tile edges, making them straight and no crossing of edges can occur. It is, therefore, easier to avoid negative tiles, If one in addition gives up the face-to-face tiling principle, the chances to tile the plane with positive tiles becomes even larger. Known examples are the Robinson triangles (![]() ) and the Danzer’s seven-fold variant. We will generalize these two examples to odd n, by making use of the following relationship
) and the Danzer’s seven-fold variant. We will generalize these two examples to odd n, by making use of the following relationship
(1) ![]()
, where ![]() is the base angle and
is the base angle and ![]() the length of the base. In terms of the apex angle
the length of the base. In terms of the apex angle ![]() the sum is over all half-rhombs with odd index. The relationship may be proven by making use of the Dirichlet Kernel
the sum is over all half-rhombs with odd index. The relationship may be proven by making use of the Dirichlet Kernel
(2) ![]()
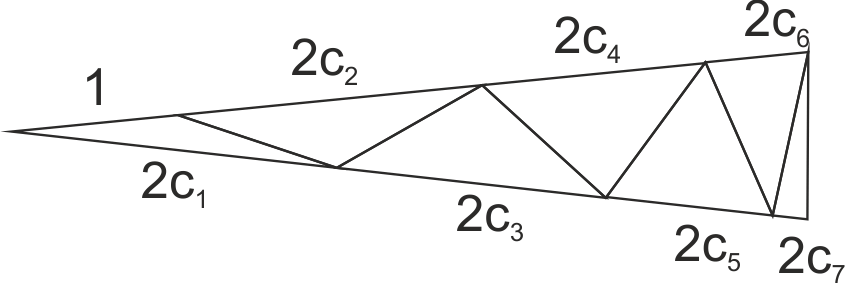
Equation 1 may be expressed as the equality between the sum of the bases of the odd half rhomb members on the one hand and the sum of the even half rhomb members plus one on the other or
(3) ![]()
In the following picture this equation is illustrated by the edges of an isosceles triangle for n=15.
If M is the inflation factor, the inflated base length of the substitution tiles is
(4) ![]()
,which is an expression in terms of the bases of some of the ![]() half-rhomb prototiles as well. Consequently, all edges, including the base edge, may be composed of a discrete number of prototile edges for all substitution tiles.
half-rhomb prototiles as well. Consequently, all edges, including the base edge, may be composed of a discrete number of prototile edges for all substitution tiles.
The substitution matrix can be determined using our model. If ![]() the general
the general ![]() substitution matrix including negative tiles is
substitution matrix including negative tiles is
(5) 
This matrix may be split up into two separate ![]() matrices for the odd and even prototiles. The one for the odd tiles can be reduced to a
matrices for the odd and even prototiles. The one for the odd tiles can be reduced to a ![]() matrix by neglecting the zero area tiles and subtracting the negative tiles from the corresponding positive ones. Below, the substitution matrices for
matrix by neglecting the zero area tiles and subtracting the negative tiles from the corresponding positive ones. Below, the substitution matrices for ![]() are given and the substitution tiles are shown in the figure.
are given and the substitution tiles are shown in the figure.
(6) ![]()
(7) 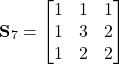
(8) 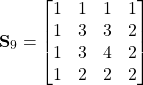
(9) 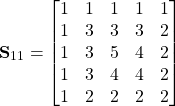
(10) 
(11) 
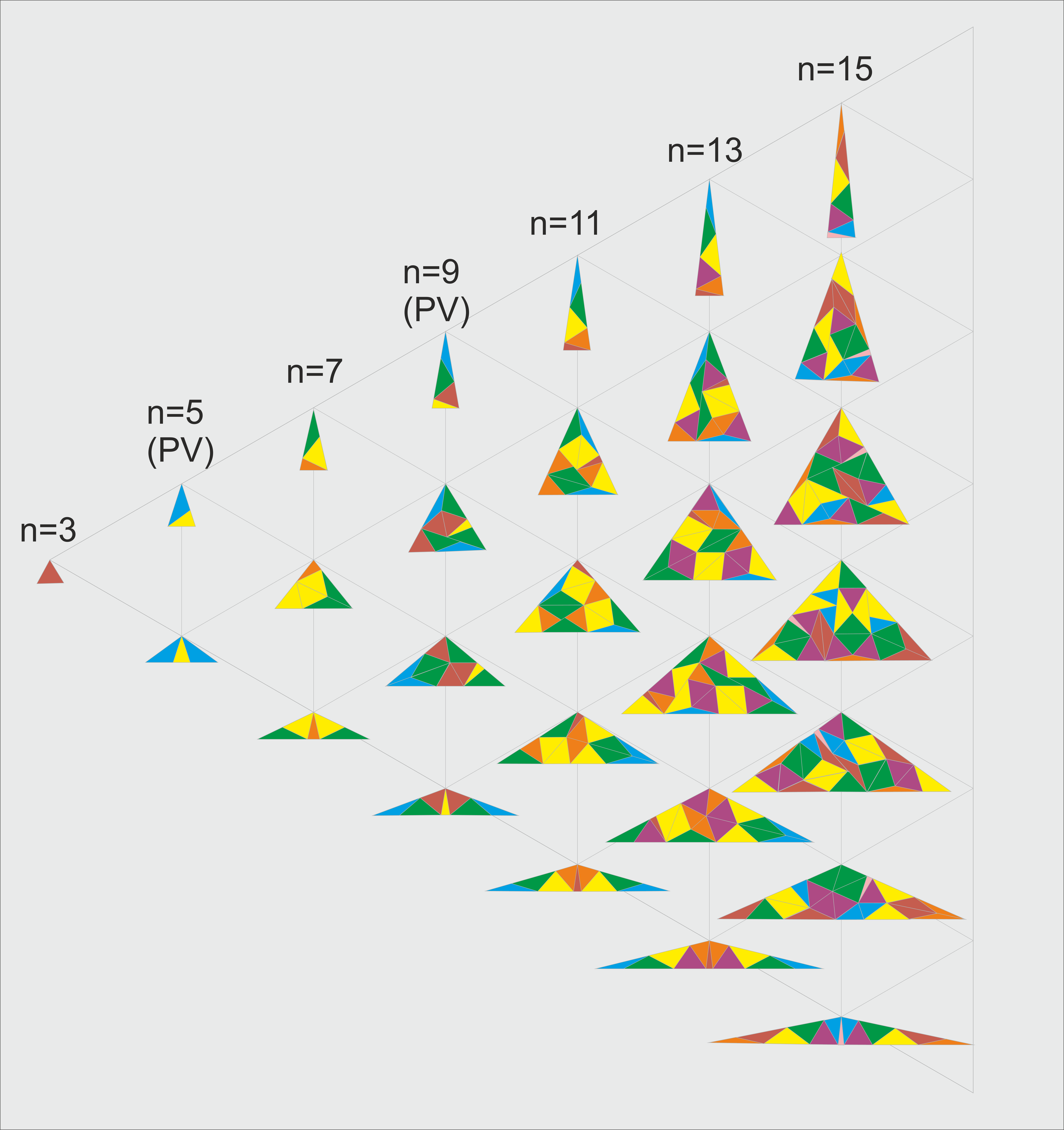
For the substitution tiles with the smallest opening angles there is only one way to arrange the prototiles. To construct the more complicated tiles a kind of “jig-saw puzzle strategy” was applied. First the tiles making up the circumference of the tile were arranged in accordance with eqs. 3 and 4. The remaining prototiles were placed in the interior by trial and error. Up to ![]() solutions have been found, but it is not clear yet whether it works for any odd
solutions have been found, but it is not clear yet whether it works for any odd ![]() .
.
The tilings are related to the Nischke-Danzer general triangle tilings for odd n (Nischke, K.-P.; Danzer, L. A construction of inflation rules based on n-fold symmetry. Discrete Comput. Geom. 15 (1996), no. 2, 221–236.
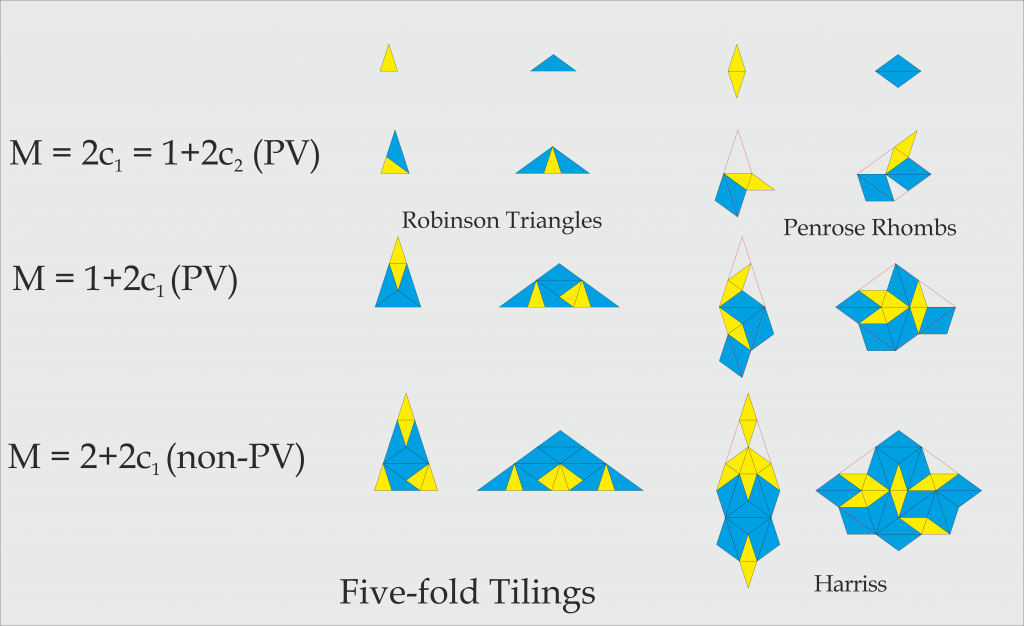
Five-fold symmetry tilings.
A summary of the five-fold isosceles triangle tilings and a comparison with rhomb tilings is shown in the next figure. Apart from the well-known Robinson triangle and Penrose rhomb tilings, new triangle tilings are shown with ![]() and
and ![]() . The corresponding rhomb tilings are Harriss
. The corresponding rhomb tilings are Harriss ![]() and
and ![]() tilings. The Harriss inflation factor is non-PV.
tilings. The Harriss inflation factor is non-PV.
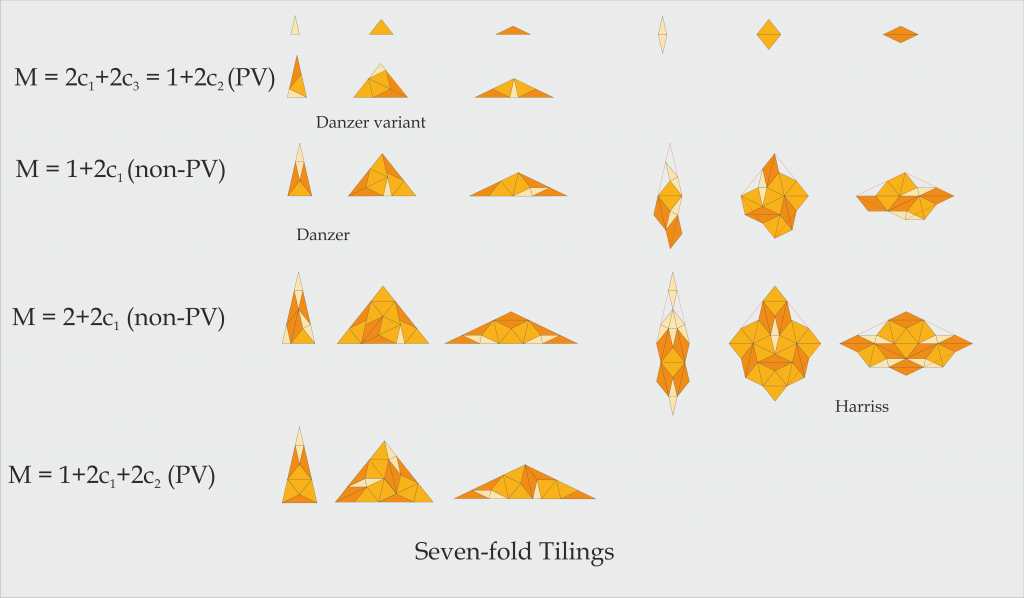
Seven-fold symmetry tilings.
Similar seven-fold triangle and some sorresponding rhomb tilings are shown in the next figure. The firs two are also shown in the aperiodic tilings encyclopedia. Although not mentioned there, the inflation factor ![]() of the first one is a PV number. The second example is from the Nischke Danzer Paper. The remaining pair of examples are new, but might be called Danzer variants as well.
of the first one is a PV number. The second example is from the Nischke Danzer Paper. The remaining pair of examples are new, but might be called Danzer variants as well.
Tilings for larger n.
n=9.
The tiling shown in fig. 2 is for ![]() or
or ![]() , having a PV inflation factor
, having a PV inflation factor ![]() . An alternative m-set is obviously
. An alternative m-set is obviously ![]() .
.
n=15.
We found a set of isosceles substitution tiles for the smallest PV number for ![]() , i.e. the one for the
, i.e. the one for the ![]() . Some of the tiles consist of prototile sets differing from the outcome of eq. 5. Due to the fact that 15 is a multiple of 5 and 3, there are special relationships between the prototiles. If we denote the area of prototile
. Some of the tiles consist of prototile sets differing from the outcome of eq. 5. Due to the fact that 15 is a multiple of 5 and 3, there are special relationships between the prototiles. If we denote the area of prototile ![]() by
by ![]() , one may easily verify that
, one may easily verify that ![]() and
and ![]() , for instance. These relationships are probably the reason why it is possible to find the complicated substitution tiles shown below. Our design strategy was again to determine the prototiles constituting the circumference first, and trying to fill in the interior of the tiles next.
, for instance. These relationships are probably the reason why it is possible to find the complicated substitution tiles shown below. Our design strategy was again to determine the prototiles constituting the circumference first, and trying to fill in the interior of the tiles next.